| المجلد 4 , العدد 4 , ذو الحجة 1427 - كانون الثاني (يناير) 2007 |
| |
| جَوْدة النتائج المخبرية السريرية |
| Quality of Clinical Laboratory Results |
| د. نجيب كيالي |
| Kayaly Najib |
| الجزء الأول: مُعَوَّلية طرق التشخيص المخبري |
| الملخص Abstract |
تتمثل المُعَوَّلية التحليلية Analytical reliability لطرق التشخيص المخبري في العناصر التالية:
- الدِّقَّة Precision التي تمثِّل قُرب نتائج القياسات المتكررة (المتوازية) لكمية ما بعضها من بعض، أي ما يسمى التكرارية Repeatability, reproducibility، والتي يتم الحكم عليها عن طريق الانحـراف المعيــاري Standard deviation.
- الضَّبْط (الصِّحَّة) Accuracy الذي يمثِّل قرب سلسلة من نتائج القياسات المتكررة من القيمة الحقيقية، والذي يتم الحكم عليه عادة من خلال فحص مادة مراقبة Control material معلومة القيمة (مصل مراقبة)، أو من خلال مقارنة نتائج الطريقة المستخدمة مع نتائج طريقة مَرجعية Reference method ذات ضبط عالٍ تم إقرارها دولياً.
- الحساسية التحليلية Analytical sensitivity التي تتحدد بمقدرة الطريقة على الكشف عن الفروق الصغيرة في تركيز المادة والتمييز بين هذه الفروق، ويُعبَّر عنها بتغيُّر الكميات المقروءة (التَّماصّ Absorbance أو غيره) خلال وَحْدة التركيز Concentration أو وحدة الفاعلية Activity، وهكذا فإن مفهوم الحساسية يختلف عن مفهوم آخر يُعرَف باسم حدّ الكشف Detection limit، وإن كان الأخير كثيراً ما يُستخدَم ليشير إلى الحساسية، وهو يمثِّل أصغر تركيز، للمادة التي يتم تحليلها، يمكن الكشف عنه.
- النوعية التحليلية Analytical specificity التي تتمثل في إمكان تعيين المادة المَعنية لوحدها فقط دون تأثُّـر ملحوظ بوجود مواد أخرى.
- قراءات الشاهد (أي الناصع أو الكَفِيء) Blank readings التي تنعكس بشكل مفيد على دقة الطرق وضبطها إذا كانت قيمها منخفضة أو متسمة بالثَّباتية والدقة العالية.
سنعرِض أيضاً المُعَوَّلية التشخيصية Diagnostic reliability لطرق التشخيص المخبري التي تتمثل في الحساسية التشخيصية والنوعية التشخيصية والقيمة التَّكَهُّنية للنتائج الإيجابية Predictive value of positive results والقيمة التَّكَهُّنيـة للنتائج السلبية Predictive value of negative results وكفاية الطريقة Efficiency of method.
تُشكِّل التقارير المخبرية السريرية دعامة هامة من دعائم تشخيص الأمراض ومتابعة سيرها وتقييم التأثير العلاجي؛ وكنتيجة لذلك فإن جَوْدة النتائج المخبرية السريرية لها دور كبير في التأثير في قرارات الطبيب المعالِج؛ ولهذا فليس مدهشاً أن يتساءل الطبيب المعالج باستمرار عن جَوْدة تلك النتائج. وهنا يبرز جلياً الواجب الملقى على عاتق الاختصاصي في التحاليل المخبرية السريرية، والمتمثل في التزامه بمراقبـة الجَوْدة Quality control بعناية بالغة بغية المساهمة الفعالة في العملية التشخيصية وفي تفسير النتائج المخبرية.
يحظى موضوع "جَوْدة النتائج المخبرية السريرية" باهتمام كبير في المختبرات السريرية في مختلف البلدان. ويلقى هذا الموضوع رعاية خاصة من الهيئات المَعنية بالمختبرات السريرية.
سنتطرق في هذا المقال إلى المواضيع التالية:
- مُعَوَّلية طرق التشخيص المخبري.
- توزُّع نتائج القياس والمَعالِم الإحصائية المميِّزة لهذا التوزع.
- المحاليل المعيارية والمنحنى المعياري.
- الأخطاء في التشخيص المخبري.
- مواد مراقبـة جَوْدة النتائـج المخبريـة
السريرية.
- مراقبة جَوْدة النتائج المخبرية السريرية.
تقسم مُعَوَّلية طرق التشخيص المخبري إلى:
- مُعَوَّلية تحليلية Analytical reliability؛
- مُعَوَّلية تشخيصيةDiagnostic reliability.
وبدل مصطلَح "المُعَوَّلية" Reliability قد يُستخدَم أحياناً مصطلح "الأداء" Performance.
|
| 1-1- المعولية التحليلية لطرق التشخيص المخبري |
إن هذه المُعَوَّلية تحدِّد جَوْدة النتائج المخبرية. وهي تتمثل بالدرجة الأولى في الدِّقَّة Precision والضَّبْط (الصِّحَّة) Accuracy، وكذلك في الحساسية التحليلية Analytical sensitivity والنوعية التحليلية Analytical specificity وقراءات الشاهد (أي الناصع أو الكَفِيء) Blank readings.
إن مصطلَحَي الدِّقَّة Precision والضَّبْط أو الصِّحَّة Accuracy يُعَدّان في بعض الأحيان بصورة خاطئة أمراً واحداً مع أن لهما في الواقع مدلولين مختلفين.
الدقة هي عبارة عن الانسجام بين نتائج القياسات المتكررة (المتوازية لكمية ما)، أو هي قُرب هذه النتائج بعضها من بعض، أي أنها تمثِّل ما يسمى التكرارية أو تكرارية الإنتاجيةRepeatability or Reproducibility.
وأما الضَّبْط (أو الصِّحَّة) فهو عبارة عن قُرب نتيجة قياس كمية ما من القيمة الحقيقية، أو قرب سلسلة من نتـائج القياسات المتكررة
(المتوازية) من القيمة الحقيقية.
إن دقة النتائج، أي تكراريتها، تتوقف على مدى تأثير ما يسمى الأخطاء العَرَضية أو الأخطاء العشوائيةAccidental or random errors، التي سيتم استعراضها لاحقاً ويتجسد تأثير هذه الأخطاء في انحراف نتائج تكرار قياس كمية ما بعضها عن بعض.
يتم الحكم على الدقة بحساب الانحراف المعياري (s).
إن تكرارية الطرق، التي تُعَدّ معياراً لدقتها، يمكن أن تكون على أنواع ثلاثة:
* تكرارية ضمن سلسلة Within-run repeatability: وهي عبارة عن القرب بين نتائج القياسات التي تجرى بشكل متوازٍ ضمن سلسلة واحدة في يوم واحد وشروط واحدة.
* تكرارية من يوم إلى يومDay-to-day repeatability: وهي عبارة عن القرب بين نتائج القياسات التي تجرى في أزمنة مختلفة (أيام متتالية) وفي شروط واحدة.
* تكرارية بين المختبرات Inter-laboratory repeatability: وهي عبارة عن القرب بين نتائج القياسات التي تجرى في مختبرات مختلفة بطريقة واحدة.
تهدف عموماً برامج ضمان مراقبة جَوْدة العمل المخبري إلى قياس دقة كل مَعلَم من المَعالِم التحليلية فيما بين المختبرات المشتركة في هذه البرامج.
من جهة أخرى فإن ضَبْط النتائج يتوقف على
مدى تأثير نوعين من الأخطاء هما الأخطاء النظامية Systematic errors والأخطاء الفادحة Gross errors.
ويتجسد تأثير الأخطاء النظامية والأخطاء الفادحة في انحراف نتيجة القياس عن القيمة الحقيقية.
وكما ذكرنا سابقاً فإن الحكم على الضبط يتم من خلال فحص مادة مراقبةControl material معلومة القيمة (مصل مراقبة)، أو من خلال مقارنة نتائج الطريقة المستخدمة مع نتائج طريقة مَرْجعية Reference method ذات ضبط عالٍ تم إقرارها دولياً.
إن الدقة والضبط مفهومان مختلفان ومستقلان تماماً لا يتوقف أحدهما على الآخر. وفي الحالة المثالية نحصل على دقة وضبط عاليين، أو بالأحرى نحصل على تكرارية جيدة للنتائج ذات قيمة متوسطة قريبة جداً من القيمة الحقيقية. إلا أن هذه الحالة لا تتحقق دوماً؛ إذ أنه يمكن أن تنشأ مشكلتان متعلقتان بالدقة والضبط:
* المشكلة الأولى هي تحقُّق دقة جيدة مصحوبة بضبط سيء، بمعنى أن تكون النتائج قريبة بعضها من بعض بحيث تتحقق دقة عالية، ولكن دون أن تكون قيمتها المتوسطة قريبة من القيمة الحقيقية (القيمة المتوسطة المضبوطة)، أي دون أن يكون الضبط عالياً. إن هذه المشكلة سهلة الحل نسبياً. وهكذا مثلاً إذا كانت دقة تعيين الغلوكوز في مصل الدم عالية، وكانت النتائج غير مضبوطة بحيث كانت تبدي دوماً انخفاضاً بمقدار 20%، فهذا يعني أن مفتاح الحل هو في إعادة اختبار المحلول المعياري أو إعادة تحضيره.
* المشكلة الثانية هي الحصول على دقة سيئة مصحوبة بضبط جيد، بمعنى أن تكون النتائج متبعثرة بشكل كبير حول قيمتها المتوسطة بحيث تعطي دقة منخفضة، ولكن دون أن تكون تلك القيمة المتوسطة بعيدة عن القيمة الحقيقية، أي مع حصول ضبط عالٍ. إن هذه المشكلة نادرة الحدوث نسبياً، إذ أن النتائج المضبوطة تبدي على الأغلب دقة عالية. وحَلّ مشكلة الدقة السيئة صعب على الأغلب نظراً لتعدد الأسباب المؤدية إلى انخفاضها: استخدام كواشف منخفضة الجَودة، حدوث خلل في الأجهزة المستخدمة، قلة مهارة القائم بالتحليل.
أما الحساسية التحليلية لطريقة ما فتتحدد بقابلية هذه الطريقة لكشف الفروق الصغيرة في تركيـز المادة أو فاعليتها والتمييز بين هذه الفروق، ويُعبَّر عنها بتغيُّر الكميات المقروءة (التَّماصّ أو غيره) خلال وحدة التركيـز أو الفاعلية، أي أنها تتناسب طرداً مع نسبة الفرق بين القيم المقروءة إلى الفرق بين التراكيز أو الفاعليات الموافقة لتلك القيم.
وهكذا مثلاً إذا أعطت طريقة تحليلية ما:
فإن النسبة:
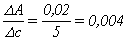هي التي تحدِّد الحساسية التحليلية.
وواضح أن نسبة 
الأعلى (الناتجة عن تغير أكبر للبسط "الصورة"، أو تغير أصغر للمقام "المَخرَج") تعني حساسية تحليلية أعلى، والعكس بالعكس.
وفي المنحنى المعياري للطريقة التحليلية تتحدد النسبة المذكورة المعبِّرة عن الحساسية بِمَيل هذا المنحنى في منطقة القياس الخطية. وأما في مناطق القياس اللاخطية، التي يكون المنحنى المعياري فيها ذا انحناء، فإن الحساسية التحليلية تتحدد بميل الأجزاء الخطية التي يتم الحصول عليها بتحليل المنحنى إلى تلك الأجزاء.
هذا ويجب التمييز بين الحساسية التحليلية وما يسمى حدّ الكشف Detection limit أو حدّ الحساسية الذي يمثِّـل أصغر تركيز للمادة التي يتم تحليلها يمكن الكشف عنه شريطة أن يعطي هذا التركيز بقياسه اختلافاً عن الشاهد (أي الناصع أو الكَفِيء) Blank الموافق باحتمال قدره 95%. ويمكن تعريف حد الكشف لطريقة ما بشكل أكثر كمية بأنه عبارة عن ثلاثـة أضعاف الانحراف المعياري S،
Standard deviation للشاهد الموافق.
قيم التَّماصّ (A) التالية: |
0.30 |
0.30 |
0.30 |
0.31 |
0.31 |
0.32 |
وقيم التركيز (c) التالية: |
100 |
101 |
102 |
103 |
104 |
105 |
أما النوعية التحليلية لطريقة ما فهي عبارة عن قابلية هذه الطريقة للانفراد في تعيين المادة أو المواد التي خُصِّصت الطريقة لتعيينها، وعدم السماح للمواد الأخرى بالدخول في التفاعل الأساسي.
وبكلمات أخرى فإن النوعية التحليلية للطريقة المستخدمة لتعيين مادة ما هي إمكان تعيين هذه المادة لوحدها فقط دون تأثُّر ملحوظ بوجود مواد أخرى في مادة الفحص (مصل الدم، مصوَّرة الدم…) أو في مزيج التفاعل، وخاصة تلك المواد القريبة سواء من حيث البنية الكيميائية المحدِّدة للخاصيات الكيميائية، أم من حيث الخاصيات الكيميائية-الفيزيائية، وكذلك دون تأثُّر يُذكَر بوجود مكوِّنات مادة الفحص نفسها كالبيليروبين والهيموغلوبين والشحميات والبروتينات، إذ أن هذه المكوِّنات تكمن فيها أسباب لخفض النوعية التحليلية، وبالتالي لنشوء أخطاء، وذلك بسبب لونها أو عَكَرها أو خواصها الأخرى.
وهكذا فإن النوعية تُعَدّ عالية إذا كان بالإمكان مثلاً مقايسة الغلوكوز في مصل الدم لوحده بوجود هِكْسوز (سكر سداسي) آخر كالمانوز، أو مقايسة البوتاسيوم لوحده في المصل (الذي يحتوي أيضاً على الصوديوم)، أو مقايسة أيّة مادة أخرى في المصل دون حصول تداخُل يُذكَر إذا كان المصل يَرَقانياً أو فيه دم منحلّ أو زيادة للشحميات.
هذا وإن التَّداخُل Interference الدوائي والتداخل الذي تسببه مكوِّنات مادة الفحص (المصل مثلاً) يُعَدّان من العوامل الهامة المؤثرة في النوعية التحليلية للطرق، وفي ضَبْطها، وبالتالي في معوليتها التحليلية. ويُقصد بالتداخل تأثر ضبط تعيين مادة ما بوجود مادة أو مواد أخرى لا تعطي بحدّ ذاتها قراءة على جهاز القياس، إلا أنها تعيق التفاعل الأساسي بسبب أُلْفَتها تجاه ناتج بَيْني لهذا التفاعل أو استهلاكها لجزء من الكاشف المستخدَم في التفاعل الأساسي.
إن تحديد النوعية التحليلية لطريقة ما يتم بدراسة تأثير المادة التي يُحتمَل أن يكون لها تأثير في النوعية، وذلك بإجراء الطريقة بوجود تراكيز مختلفة من المادة التي يُدرَس تأثيرها مع البدء بالتركيز الموافق للحد الأعلى المحتمل وجوده على الصعيد السريري، ثم تحديد الفرق بين التركيز الفعلي للمادة التي يتم تعيينها والتركيز المَقيس بوجود المادة التي يُدرَس تأثيرها. فإذا كان هذا الفرق ذا شأن (معتداً به) فيجب عندئذ تحديد الحد الذي يبدأ عنده هذا التأثير.
الآن وقبل الحديث عن قراءات الشاهد (أي الناصع أو الكَفِيء) Blank باعتبارها أحد العوامل المؤثرة في المعولية التحليلية سنتطرق إلى مفهوم الشاهد بحد ذاته لما له من أهمية بالغة في الكيمياء السريرية.
إن الشـاهد (أي الناصع أو الكَفِيء) Blank
هو بالتعريف مِحفَد (مِركَن) Cuvette (أي أنبوب خاص للقياس الضوئي) لا غنى عنه يُستخدَم لدى مقايَسة العيِّنة Sample والمِعْياري Standard، ويتم بوساطته حذف استجابة جهاز القياس الناجمة عن التأثير اللوني أو غير اللوني للكواشف والمذيب والعيِّنة، والتي تعني في القياس الضوئي Photometry التماصِّ Absorbanc, A، وذلك للإبقاء على الاستجابة الناتجة عن التفاعل النوعي المعني حصراً؛ ومعنى ذلك في القياس اللوني Colorimetry حذف قراءة لون الكواشف ولون العيِّنة للإبقاء فقط على لون الناتج الذي يهمنا؛ ويتأتى ذلك باستخدام الشاهد لِمُعاوَرة Calibration جهاز القياس قبل البدء بعملية القياس.
تتمثل الشواهد (أي النواصع أو الكفيئات) Blanks في مَحافِد (مَراكِن) Cuvettes يوضع فيها حجم من السوائل المستخدَمة في الطريقة هي إما الكواشف دون العيِّنة، أو هي الكواشف مع العيِّنة شريطة تغييب الدور التفاعلي للمكوِّن الذي يَجري تحليله، أو هي المذيب فقط، أو لا يوضع فيها شيء، أي تمثِّل مَحافِد (مَراكِن) فارغة غير مُخْلاة من الهواء.
وتبعاً لمحتوى الشواهد (أي النواصع أو الكفيئات) المستخدَمة في الكيمياء السريرية
فهي تُقسَم إلى أربعة أنواع:
- شاهد الكواشف Reagent blank؛
- شاهد العيِّنة Sample blank؛
- المذيب (الماء المقطَّر أو غيره)؛
- الهواء.
يُعَدّ شاهد الكواشف Reagent blank, RB أنسب الشواهد وأكثرها شيوعاً، وهو عبارة عن محلول يحتوي على المذيب والكواشف التي تُستخدَم في تحضير محلول اختبار العيِّنة ومحلول الاختبار المعياري، ولكن باستثناء المادة التي أُعِدّ الاختبار لتعيينها. ولهذا فإن استجابة جهاز القياس لدى وضع شاهد الكواشف فيه تعزى إلى مواد أخرى مختلفة عن المادة التي يتم تعيينها وعن ناتج تفاعلها، أي أن القراءة التي يشير إليها الجهاز عندئذ يجب أن تمثِّل القراءة "صفر" التي توافق تركيزاً للمادة التي يُجرى فحصها مقداره "صفر". وهكذا مثلاً إذا وُضِع مقياس اللون المستخدَم للقياس الضوئي على التَّمَاصّ Absorbanc, A "صفر" أو الامتراق النسبي المئوي (أي الإنفـاذية أو النفوذية النسـبية المئويـة Percent Transmittance, Percent Transmission, %T "100" لدى وجود شاهد الكواشف فيه فإن ذلك سيجعل أيَّة استجابة لاحقة على لوحة القراءة ناجمةً فقط عن تأثير المادة التي يتم تعيينها، أي أن التَّماصّ الذي سيُقرَأ لدى وضع محلول اختبار العيِّنة (أو محلول الاختبار المعياري) في المقياس سيمثِّل تماصّ المادة التي يتم تعيينها أو ناتج تفاعلها دون أن يشمل تماصّ المذيب والكواشف التي تم استخدامها نظراً لأن هذا التَّماصّ قد تم حذفه بعملية تصفير الجهاز بوجود شاهد الكواشف فيه، أي بعملية معاوَرة Calibration الجهاز. وفي بعض الحالات يمكن ألاّ يُعتمَد على شاهد كواشف اعتماداً مباشراً، إذ يُلجَأ إلى الاعتماد عليه بشكل غير مباشر، وذلك بمعاوَرة الجهاز على الصفر بواسطة المذيب الموافق (الماء المقطر أو غيره)، ثم قراءة تماصّ شاهد الكواشف، وأخذ هذا التَّماصّ بعين الاعتبار لدى حساب النتائج، حيث يُطرَح من تماصّ محلول اختبار العيِّنة، وكذلك من تماصّ محلول الاختبار المعياري، أي تُجرى عمليتا الطرح (AS – ARB) و (ASt – ARB). وهنا يجدر التنويه بأنه لا يجوز إجراء عملية الطرح هذه باستبدال التماصّات بالامتراقات (أي النفوذيات) النسبية المئوية لأن ذلك من شأنه أن يؤدي إلى الوقوع في الخطأ.
أما بالنسبة إلى شاهد العيِّنة Sample blank, SB فهو يُستخدَم في القياس الضوئي في بعض الأحيان عندما تكون هناك ضرورة لحذف تأثير لون العيِّنة بالذات في تماصّ اللون الناتج عن تفاعل المادة التي يتم تعيينها. وشاهد العيِّنة هو عبارة عن محلول يحتوي على العيِّنة التي يتم فحصها، خلافاً لشاهد الكواشف، كما يحتوي على المذيب والكواشف المستخدمة كلها باستثناء أحد الكواشف الذي يَحُول غيابه دون حصول التفاعل الأساسي، وأحياناً دون استثناء لأيّ من الكواشف شريطة أن تتم إعاقة لنشوء التفاعل الأساسي بطريقة أو بأخرى. ولهذا فإن استجابة مقياس اللون لدى وضع شاهد العيِّنة فيه هي هنا أيضاً غير ناجمة عن الناتج الذي تعطيه المادة التي يتم تعيينها لأن هذه المادة - على الرغم من وجودها في الشاهد - لا تخضع للتفاعل الأساسي. وهكذا فإن وضع مقياس اللون على التَّماصّ "صفر" لدى وجود شاهد العيِّنة فيه سيجعل أيّ تماصّ لاحق ناجماً عن تأثير المادة التي يتم تعيينها فقط، أي كما هو عليه الحال لدى تصفير المقياس بواسطة شاهد الكواشف.
إلاّ أنه يجدر التنويه هنا بأن هناك حالات لا يمكن فيها الاستهانة بتأثير الكاشف الذي ينبغي أن يخلو منه شاهد العيِّنة. ولهذا فإنه لا يكفي في مثل هذه الحالات الاعتماد على شاهد العيِّنة لوحده فقط، بل يلزم عندئذ شاهد كواشف بالإضافة إلى شاهد العيِّنة. وتتم معاورة مقياس اللون على الصفر في هذه الحالات بوساطة شاهد الكواشف، ثم يقاس تماصّ شاهد العيِّنة، ويؤخذ هذا التَّماصّ بعين الاعتبار لدى حساب النتائج.
أما بالنسبة إلى استخدام المذيب (الماء المقطر أو غيره) كشاهد فهو يتم عادة في الحالات التي لا يكون فيها للكواشف المستخدَمة تأثير يُذكَر في القراءة الخاصة بتفاعل المادة التي يتم تعيينها. ولهذا فإن استجابة المقياس لدى وضع المذيب فيه ناجمة فقط عن تأثير المذيب وتأثير المادة التي صُنِع منها المِحفَد (المِرْكَن) Cuvette أيضاً، أي يجب أن تكون القراءة التي يشير إليها المقياس عندئذ "صفراً"، وتُوافِق تركيزاً للمادة التي يجري تعيينها مقداره صفر. وهكذا فإن تصفير المقياس لدى وجود المذيب فيه سيجعل أيّة استجابة لاحقة على لوحة القراءة ناجمةً فقط عن تأثير المادة التي يتم تعيينها، أو تأثير المعياري.
أما بالنسبة إلى الهواء كشاهد فيُستخدَم في المقياس الضوئي الطَّيْفي Spectrophotometer في المنطقة فوق البنفسجية UV، حيث لا يكون للمذيب والكواشف المستخدَمة تأثير في تماصّ المركَّب الناتج عن تفاعل المادة التي يتم تعيينها، ويتم تصفير المقياس عندئذ بحيث يوضع فيه مِحفَد Cuvette فارغ، أي يحتوي على الهواء؛ والتَّماصّ الذي يظهر على المقياس هنا، أي لدى وضع المِحفَد الفارغ فيه، ناجم عن تأثير المادة التي صُنِع منها هذا المِحفَد. وبكلمات أخرى فإن شاهد الهواء هو مِحفَد فارغ غير مُخْلى من الهواء).
والآن ما هو تأثير قراءاته في المعولية التحليلية للطرق.
إن لقراءات الشاهد الكفيء Blank تأثيراً كبيراً في دقة الطرق وضبطها. وهذا التأثير بسيط ومفيد جداً إذا كانت تلك القراءات متدنية. وأما إذا كانت قراءاته عالية فهي لا يمكن أن تجعل دقة الطرق وضبطها مُرْضيين إلا إذا اتسمت بالثَّباتية والدقة العالية لأن ذلك من شأنه أن يسمح بالتقاط الفروق الصغيرة بين القياسات. إن مثل هذه القراءات العالية لشاهد الكواشف تُلاحَظ في بعض الطرق المطَبَّقة في الكيمياء السريرية كطريقة كومبلِكسون الأورتو-كرِزول فتالِئين لتعيين الكالسيوم، التي تُعَدّ ذات معولية جيدة فيما لو استُخدِمت للعمل أدوات لدائنية نَبُوذة Disposable plastics، أي تُستعمَل لمرة واحدة فقط، أو أدوات زجاجية منظَّفة بطريقة مناسبة بواسطة محلول ثنائي الكرومات المنظِّف أو حمض كلور الماء ذي التركيز 0.5 مول/ل للتخلص من الشوارد) دون استخدام الماء العادي كي لا يحصل تلوُّث بالكالسيوم ذي المنشأ الخارجي. وتجدر الإشارة هنا إلى أن غياب النظافة المناسبة اللازمة لتعيين الكالسيوم يمكن أن يجعل قراءة شاهد الكواشف عالية بحيث تؤدي إلى معولية سيئة، بل يمكن أن يجعل هذه القراءة العالية تصل إلى حدّ مفرِط يفوق قراءة محلول اختبار العيِّنة أو محلول الاختبار المعياري، الأمر الذي يؤدي إلى استحالة المقايسة. |
| 1- 2- المعولية التشخيصية لطرق التشخيص المخبري
|
إن المعولية التشخيصية لطرق التشخيص المخبري هي التي تحدِّد اختيار الطرق ذات المعولية التحليلية الجيدة؛ فمن بين الطرق الكثيرة العدد يجب اختيار تلك الطرق التي تتسم بمعولية تشخيصية جيدة تساعد على حل المهمات الأساسية الملقاة على عاتق الطبيب المعالِج، وهي: تفريق حالات الصِّحَّة عن المرض، والكشف عن الفعاليات المَرَضية في مراحل تطورها المبكِّرة، وتحديد طبيعة إصابة الجسم ودرجة هذه الإصابة.
إن المعولية التشخيصية لطرق التشخيص المخبري تتمثل في الحساسية التشخيصية Diagnostic sensitivity والنوعية التشخيصية Diagnostic specificity والقيمة التَّكَهُّنية للنتائج الإيجابية Predictive value of positive results والقيمة التَّكَهُّنية للنتائج السلبية Predictive value of negative results وكفايـة الطريقـة Efficiency of method.
إن الحساسية التشخيصيةDiagnostic sensitivity لطريقة تحليلية ما في مرض معيَّن
تتمثل بالنسبة المئوية لتواتـر النتائج الإيجابية فعلاً لدى المصابين بهذا المرض، أي تواتر النتائج الإيجابية نسبةً إلى النتائج كلها لدى المصابين بالمرض المَعني، والتي تشمل النتائج الإيجابية الناجمة عن هذا المرض والنتائج السلبية الكاذبة في وجود هذا المرض. وهكذا مثلاً يقال إن الحساسية التشخيصية لطريقة ما لدى مرض معيَّن هي 97% إذا كان تواتر النتائج الإيجابية لهذه الطريقة في هذا المرض هو 97%، أي إذا كانت النتائج إيجابية بالفعل بنسبة 97% وسلبية بشكل كاذب بنسبة 3%. ويمكن أن يُعبَّر رياضياً عن هذا التعريف للحساسية التشخيصية بالعلاقة التالية:
الحساسية التشخيصية =
النسبة المئوية للإيجابية عند المرض = |
عدد النتائج الإيجابية فعلاً |
× 100 |
العدد الكلي للنتائج لدى المصابين بالمرض |
= |
عدد النتائج الإيجابية فعلاً |
× 100 |
عدد النتائج الإيجابية فعلاً + عدد النتائج السلبية الكاذبة |
أما النوعية التشخيصيةDiagnostic specificity لطريقة تحليلية ما بالنسبة إلى مرض معيَّن فتتمثل بالنسبة المئوية لتواتر النتائج السلبية لدى غير المصابين بهذا المرض، أي تواتر النتائج السلبية فعلاً نسبةً إلى النتائج كلها لدى غير المصابين بالمرض المَعني سواء كانت هذه النتائج سلبية فعلاً أم إيجابية كاذبة. وهكذا مثلاً فإنه يقال إن النوعية التشخيصية لطريقة ما بالنسبة إلى مرض معيَّن هي 95% إذا كان تواتر النتائج السلبية لدى غير المصابين بهذا المرض هو 95%، أي إذا كانت النتائج لدى غير المصابين بهذا المرض سلبية بنسبة 95% وإيجابية بشكل كاذب بنسبة 5%. ويمكن أن يُعبَّر رياضياً عن هذا التعريف للنوعية التشخيصية بالعلاقة التالية:
النوعية التشخيصية =
النسبة المئوية للسلبية لدى غياب مرض معين = |
عدد النتائج السلبية فعلاً |
× 100 |
العدد الكلي للنتائج لدى غير المصابين |
= |
عدد النتائج السلبية فعلاً |
× 100 |
عدد النتائج السلبية فعلاً + عدد النتائج الإيجابية الكاذبة |
هذا وكثيراً ما يُفهَم بمصطلَح النوعية التشخيصية للطريقة المستخدَمة لتشخيص مرض ما "مدى إيجابية الطريقة في الحالات الأخرى المَرضية وغير المَرضية، وكذلك عدد تلك الحالات التي تظهر فيها الإيجابية". وهكذا فإن الطريقة تُعَدّ ذات نوعية تشخيصية عالية إذا لم تُبدِ نتائج إيجابية قوية في حالات أخرى غير الحالة المَرضية المَعنية وإذا لم يكن طيف تلك الحالات (عددها) واسعاً.
ومن الجدير بالإشارة أن الاختبار المستخدَم لتشخيص مرض معيَّن يُعَدّ اختباراً مثالياً من الناحية التشخيصية إذا كانت كلّ من حساسيته ونوعيته التشخيصيتين 100%، أي إذا كانت أيّة نتيجة من النتائج الشاذة (المرتفعة أو المنخفضة) لهذا الاختبار ستكشف بالفعل عن المصابين بالمرض المَعني. إلاّ أنه لا توجد للأسف مثل هذه الاختبارات المثالية التي تمتاز بحساسية ونوعية مُطْلَقتين. وتُستثنى من ذلك الاختبارات الوصفية البحتة، أي التي تصف حالات معيَّنة، كما هو عليه الحال بالنسبة إلى اختبارات تعيين المستويات المصلية لهرمون الثيروكسين T4 وهرمون ثلاثي يود الثيرونين T3 والهرمون المنبِّه للدَّرَقية (الحاثَّة الدرقية) TSH التي تُستخدَم لتشخيص فَرْط الدرقية أو قُصورها، وكذلك اختبار تعيين المستوى المصلي للبوتاسيوم لدى استخدامه لوصف حالة نقص البوتاسَمية، واختبار تعيين الهيموغلوبين في الدم لدى استخدامه لتشخيص فقر الدم…، علماً بأن الاختبارات الوصفية لم تعد قليلة.
وأما القيمة التكهُّنية للنتائج الإيجابية Predictive value of positive results، التي يشار إليها اختصاراً في أحيان كثيرة بعبارة القيمة التكهُّنية فقط، فتتمثل بالنسبة المئوية لتواتر النتائج الإيجابية لهذه الطريقة لدى المصابين بالمرض المَعني، أي تواتر النتائج الإيجابية فعلاً نسبةً إلى النتائج الإيجابية كلها سواء كانت إيجابية فعلاً ناجمة عن المرض المَعـني أم إيجابية بشكل كاذب غير ناجمة عن هذا المرض. ويمكن أن يُعبَّر رياضياً عن هذا التعريف للقيمة التكهُّنية للنتائج الإيجابية بالعلاقة التالية:
القيمة التكهنية للنتائج الإيجابية =
النسبة المئوية للنتائج الإيجابية فعلاً إلى النتائج الإيجابية ككل = |
عدد النتائج الإيجابية فعلاً |
× 100 |
العدد الكلي للنتائج الإيجابية |
أي أن: القيمة التكهنية للنتائج الإيجابية = |
عدد النتائج الإيجابية فعلاً |
× 100 |
عدد النتائج الإيجابية فعلاً + عدد النتائج الإيجابية الكاذبة |
وهكذا فإن القيمة التكهُّنية للنتائج الإيجابية تتمثل كالحساسية التشخيصية في عدد النتائج الإيجابية فعلاً، إلاّ أن هذا العدد يُنسَب لدى القيمة التكهُّنية إلى عدد النتائج الإيجابية كلها، سواء كانت ناجمة عن المرض المَعني، أي إيجابيـة فعلاً، أم عن غير المرض المَعني، أي إيجابية كاذبة، وذلك خلافاً لما هو عليه الحال لدى الحساسية التشخيصية، حيث يُنسَب عدد النتائج الإيجابية فعلاً إلى العدد الكلي للنتائج لدى المصابين بالمرض المَعني فقط، سواء كانت هذه النتائج إيجابية فعلاً أم سلبية بشكل كاذب، وليس إلى العدد الكلي للنتائج الإيجابية الناجمة عن المرض المَعني أو عن غيره.
هذا ومن الواضح أن القيمة التكهُّنية للنتائج الإيجابية (أي عدد النتائج الإيجابية فعلاً نسبةً إلى عدد النتائج الإيجابية كلها) تتوقف على الحساسية التشخيصية (أي على عدد النتائج الإيجابية فعلاً نسبةً إلى عدد النتائج الإيجابية فعلاً والسلبية كَذِباً في المرض المَعني)، كما تتوقف على النوعية التشخيصية (أي على عدد النتائج السلبية فعلاً نسبةً إلى عدد النتائج السلبية فعلاً والإيجابية زَيْفاً في المرض المَعني).
ومما لاشك فيه أن القيمة التكهُّنية للنتائج الإيجابية تتوقف على معدَّل انتشار Prevalence المرض المَعني ضمن الجَمهرة التي يَجري فحصها، فهذه القيمة ترتفع بارتفاع معدل انتشار المرض ضمن الجمهرة. وهكذا مثلاً إذا كان معدل انتشار مرض كبدي وسط جمهرة ما منخفضاً، وطُبِّق على هذه الجمهرة اختبار لوظيفة الكبد يمتاز بحساسية تشخيصية عالية وبنوعية تشخيصية عالية أيضاً، فإن القيمة التكهُّنية للنتائج الإيجابية لهذا الاختبار يمكن أن تكون منخفضة. وأما إذا طُبِّق الاختبار نفسه على جمهرة أخرى تتضمن أشخاصاً كحوليين، فإن القيمة التكهُّنية للنتائج الإيجابية لهذا الاختبار يمكن أن ترتفع بشكل كبير.
هذا ويمكن أن تُحسَب القيمة التكهُّنية للنتائج الإيجابية تبعاً لمعدل انتشار المرض وللحساسية والنوعية التشخيصيتين اعتماداً على العلاقة الرياضية المبينة أدناه:
وهكذا مثلاً إذا كان معدل انتشار المرض 50%، وكانت الحساسية التشخيصية 95%، والنوعية التشخيصية 75%، فإن القيمة التكهّنية للنتائج الإيجابية يمكن حسابها كما يلي:
القيمة التكهنية للنتائج الإيجابية = |
معدل الانتشار × الحساسية التشخيصية |
(معدل الانتشار × الحساسية التشخيصية) + (1 – معدل الانتشار) (1 – النوعية التشخيصية) |
القيمة التكهنية للنتائج الإيجابية = |
0.50 × 0.95 |
= |
0.475 |
= |
0.475 |
(0.50 × 0.95) + (1 – 0.50)(1 – 0.75) |
0.475 + 0.125 |
0.6 |
أي أن: القيمة التكهّنية للنتائج الإيجابية = 0.792، أي 79.2%.
إن القيمة التكهّنية للنتائج الإيجابية تُوْلى لها أهمية خاصة في التطبيقات السريرية، إذ أنها تكشف عن النسبة المئوية للأشخاص الذين يُفترَض في البدء أنهم إيجابيون بالنسبة إلى مرض معيَّن، ثم تأتي نتائج الاستقصاءات التشخيصية المفصَّلة لتثبت في النهاية أنهم مصابون فعلاً بالمرض المَعني.
أما القيمة التكهُّنية للنتائج السلبية Predictive value of negative results لطريقـة تحليليـة ما فتتمثل بالنسـبة المئوية
لتواتر النتائج السلبية لهذه الطريقة لدى غير المصابين بالمرض المَعني، أي تواتر النتائج السلبية فعلاً نسبةً إلى النتائج السلبية كلها سواء كانت سلبية فعلاً ناجمة عن غياب المرض المَعني أو سلبية كاذبة ناجمة عن سبب آخر. وهكذا فإن القيمة التكهّنية للنتائج السلبية تتمثل في تواتر الأشخاص المفحوصين غير المصابين بالمرض المَعني ضمن الأشخاص الذين يُبدون نتائج سلبية. ويمكن أن يُعبَّر رياضياً عن هذا بالعلاقة المبينة أدناه:
القيمة التكهُّنية للنتائج السلبية = النسبة المئوية للنتائج السلبية فعلاً إلى النتائج السلبية ككلّ = |
= |
عدد النتائج السلبية فعلاً |
× 100 = |
العدد الكلي للنتائج السلبية |
= |
عدد النتائج السلبية فعلاً |
× 100 |
عدد النتائج السلبية فعلاً + عدد النتائج السلبية الكاذبة |
وأما كفاية الطريقة Efficiency of method فتتمثل بالنسبة المئوية للنتائج الفعلية، الإيجابية منها والسلبية، أي التي تتجاوب مع حالات الأشخاص المفحوصين الفعلية، أي النسبة المئوية للنتائج التي يُصنَّف الأشخاص المفحوصون على أساسها بشكل صحيح كأشخاص مصابين بالمرض المَعني وأشخاص غير مصابين بهذا المرض. ويمكن التعبير عن هذا التعريف لكفاية الطريقة بالعلاقة التالية:
كفاية الطريقة = النسبة المئوية للأشخاص المصنَّفين فعلاً كمصابين وغير مصابين =
= |
عدد النتائج الفعلية |
× 100 = |
العدد الكلي للنتائج الفعلية والكاذبة |
= |
عدد النتائج الإيجابية الفعلية + عدد النتائج السلبية الفعلية |
× 100 |
عدد النتائج الإيجابية الفعلية + عدد النتائج الإيجابية الكاذبة + عدد النتائج السلبية الفعلية + عدد النتائج السلبية الكاذبة |
|
| |
| الجزء الثاني- توزُّع نتائج القياس والمَعالِم الإحصائية المميِّزة لهذا التوزع |
| الملخص Abstract |
سنتطرق في هذا الجزء إلى توزع نتائج القياس لدى تطبيق الطرق التحليلية المختلفة، وإلى المَعالِم الإحصائية Statistical parameters الثلاثة المميِّزة لهذا التوزع:
1- القيمة المتوسطة Mean value لنتائج القياسات المتكررة لكمية معينة، التي تدعى تجاوزاً "القيمة الحقيقيـة" True value، وتمييز هذه القيمة عن القيمة الناصفة Median value والقيمة السائدة Mode.
2- الانحراف المعياري Standard deviations المميِّز لتبعثر القيم المَقيسة حول القيمة المتوسطة، وبالتالي للدِّقة Precision، أي لقُرب نتائج القياسات المتكررة (المتوازية) لكمية ما بعضها من بعض.
3- مُعامِل الاختلاف Coefficient of variation, CV المميِّز أيضاً للدقة، والذي يمكِّن كذلك من المقارنة بين جَوْدة النتائج التي تعطيها الطرق المختلفة.
|
غنيّ عن البيان أنه لدى إجراء قياسات متكررة لمكوِّن معيَّن يمكن أن نحصل على نتائج مختلفة نوعاً ما. وهكذا مثلاً إذا قسنا كمية ما فإننا يمكن أن نحصل على نتيجتين تبدوان "متساويتين" إذا عُبِّر عنهما بأرقام صحيحة، ولْتكـن هاتان النتيجتان 10.0 و 10.0، ولكن إذا عبَّرنا عن النتائج مستخدمين الرقم الأول بعد الفاصلة فإن هاتين النتيجتين يمكن أن تكونا مختلفتين، ولْنَقلْ أنهما مثلاً 9.1 و 10.1. وعلى الرغم من أن هذا الاختلاف بين النتائج يمكن ضبطه إلى حدّ ما، مثلاً بإجراء القياسات في درجة حرارة ثابتة وفي شروط معيارية أخرى، إلاّ أنه لا يمكن جعل النتائج متطابقة تماماً، ذلك أن هناك تغيّرات عَرَضية Accidental لا يمكن ضبطها تساهم مع عوامل عديدة أخرى معلومة أو مجهولة، في التأثير في النتائج مسببةً فروقاً عَرَضية فيما بينها. ومن ناحية أخرى فإن هذه النتائج المختلفة تجمع فيما بينها قيمة مشتركة تتموَّج حولها النتائج. وهكذا فإن الفروق العَرَضية بين النتائج تبرز باعتبارها انحرافات عَرَضية للكمية المَقيسة أو ما نسميه أخطاء عَرَضية Accidental errors. إن معرفة هذه الأخطاء لها أهمية خاصة من الناحية العملية، وهذه المعرفة يمكن أن تتحقق فيما لو كان بالإمكان معرفة القيمة الحقيقية True value، إلاّ أن ذلك غير ممكن للأسف حتى لو كانت الطريقة المستخدمة ذات مُعَوَّليَّة Reliability عالية، وذلك بسبب عدم معرفتنا للأخطاء العَرَضية التي ستحصل. ولهذا بالذات فإن القيمة الحقيقية تُسمَّى تجاوزاً بهذا الاسم، ويُقصد بها القيمـة المتوسِّـطة Mean value لنتائج القياسات المتكررة.
لِنُجرِ في شروط متماثلة قدر ما يمكن عدّة اختبارات متكررة، مثلاً 9 اختبارات، وذلك لتعيين كمية ثابتة مجهولة µ، ولنفترض أننا حصلنا على القيم التالية:
47 49 49 50 50 50 51 51 52
إن هذه النتائج تقدِّر كمية حقيقية واحدة هي µ، ويحتوي كلّ منها على معلومة معيَّنة عن هذه الكمية، إلاّ أن تبعثر النتائج لا يعطينا أساساً لاتخاذ قرار بأن قيمة µ مساوية لأيّ منها. ومع ذلك فإن لنا الحق في اعتبار أن قيمةµ تقع بين النتيجتين النهائيتين 47 و52، وكذلك فإنه يمكننا أن نتوقع بتحفُّظ أنها قريبة من القيمة 50
نظراً لأن هذه القيمة تتكرر ثلاث مرات.
وعلى الرغم من ذلك فإن الطريقة الوحيدة للحصول على معرفة أفضل لقيمة µ هي زيادة عدد القياسات، ذلك لأن هذه الزيادة من شأنها أن تجعل النتائج متمركزة أكثر حول قيمة µ. ومن الطبيعيّ أن نتوقع أنه بزيادة عدد القياسات ستظهر نتائج جديدة مشابهة للنتائج التسع الأولى، ولكن مع احتمال توسُّع الفرق بين النتيجتين النهائيتين وظهور النتيجة البَيْنية 48، التي لم تكن موجودة ضمن النتائج التسع الأولى.
لنفترض الآن أن عدد القياسات قد زاد بحيث أصبح 20 قياساً، ولنوزع النتائج كلها بشكل مجموعات يتضمن كل منها النتائج المتساوية القيمة، وذلك كما هو مبين أدناه:
عدد النتائج المتكررة (التواتر) f ) : |
1 |
2 |
4 |
6 |
4 |
2 |
1 |
قيمة كل مجموعة من النتائج (x) : |
47 |
48 |
49 |
50 |
51 |
52 |
53 |
|
إن كل قيمة ْXi تتضمن في الحقيقة القيم التي تقع ضمن المجالx ±0,5. وهكذا هو الحال مثلاً مع القيم من 46.5 حتى 47.5، التي لم تُسجَّل في الجدول المذكور أعلاه، والتي قُرِّبت إلى القيمة 47 لدى القياس، وكذلك الأمر بالنسبة إلى القيم من 47.5 حتى 48.5 المقرَّبة إلى القيمة 48… وهلمّ جرّاً. وهذا يعني أن كل نتيجة تمثِّل توزعاً ضمن مجال مركزه القيمة التقريبية (المقرَّب إليها)، التي تمثِّل قيمة متوسِّطة، في حين أن عرضه هو Δx = 1 .
هذا ويمكننا تمثيل المعطيات السابقة بيانياً باستخدام ورق بيانيّ خطيّ بحيث نمثل على محور العينات الشاقولي عدد النتائج المتساوية القيمة التي تتضمنها كل مجموعة، أي التواترFrequency (f)، كما نمثل على محور السينات الأفقي القيم x، ثم نرسم خطوطاً أفقية موافِقة لكل تواتر فوق المجالاتΔx = 1، أي فوق القيـم 47 ±0,5، 48 ± 0,5 …، وبعدها نصل الخطوط الأفقية الحاصلة بخطوط شاقولية، وبذلك نحصل على خط منكسر مدرَّج يُدعى مُنَسَّج توزُّع التواترFrequency distribution histogram. وهذا المنسَّج يُرسَم غالباً بشكل مستطيلات يتم الحصول عليها بتمديد الخطوط الشاقولية حتى محور السينات كما في الشكل 1.
إن منسَّج توزُّع تواتر النتائج يبيِّن أن النتائج تتركز حول قيمة متوسِّطة Mean value للكمية µ تقع حيثما يكـون تواتر النتائج أكبر ما يمكن، وهذه القيمة المتوسطة هي في مثالنا بين 49.5 و 50.5.
لنفرض الآن أنه كان لدينا عدد لانهائيّ من النتائج، وليس عدداً محدَّداً (20 أو غيره). فإذا وزعنا هذه النتائج بشكل مجموعات أيضاً فإننا سنحصل على مجالات لتوزُّع النتائج لانهائية في الصغر، وبالتالي فإن درجات المنسَّج الذي سيتم الحصول عليه ستكون ضيقة بشكل لانهائيّ (يتناهى إلى الصفر)، وسيتحول المنسج الحاصل إلى منحنى متصل. إن هذا المنحنى المتصل يُدعى منحنى توزُّع التواترFrequency distribution curve. وفي معظم الحالات، كما هو الحال في مثالنا الوارد هنا، فإن منحنى توزع التواتر هو منحنى له شكل الناقوس Bell shaped، ويُرسَم اعتماداً على أنه متناظر حول ذروته (نهايته العظمى) التي يتركز عندها أكبر عدد من النتائج، والتي يُفترَض أن إحداثيَّها السينيّ يمثِّل القيمة المتوسطة للكميةµ، ويُدعى هذا المنحنى بالمنحنى السَّويّ أو منحنى غاوسNormal or Gaussian curve؛ وهو موضَح في الشكل رقم (2)، ويتميز بالتناظر حول القيمة المتوسطة التي تمثل ذروة المنحنى مع وجود عدد متساوٍ من النتائج أكبر من هذه القيمة وأصغر منها.
مما تقدَّم نلاحظ أن القيمة المتوسطة Mean value لنتائج القياسات المتكررة للكمية µ
|
الشكل 1: مُنَسَّج توزُّع تواتر 20 نتيجة.
الشكل 2: منحنى غاوس. |
يجب اعتبارها القيمة
الحقيقية True value لهذه
الكمية، وهي تُعَدّ مَعْلماً هاماً مميِّزاً لمنحنى توزع التواتر؛ فهي القيمة التي
توافق ذروة هذا المنحنى، وهي بالتعريف المتوسط الحسابي للقيم كلها، ويُرمَز لها بـ  ، وتُحسَب بتقسيم مجموع القيم الفردية كافـةً  على عدد القيم:
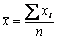
وبكلمات
أخرى فإن القيمة الحقيقية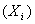 هي القيمة المتوسطة () لعدد لانهائي من النتائج.
هذا ويجب تمييز القيمة المتوسطة Mean value عن قيمتين أخريين تُدعيان القيمة الناصفة Median value والقيمة السائدة Mode.
إن القيمة
الناصفة هي عبارة عن القيمة التي تقع في منتصف سلسلة من المعطيات.
وأما القيمة
السائدة فهي ذلك المتحوِّل الذي يتكرر ظهوره أكثر بين المعطيات، ولهذا فإن القيمة
السائدة يمكن أن تكون أيّة قيمة في سلسلة المعطيات. ولإيضاح الفروق بين القيمة المتوسطة والقيمتين الناصفة والسائدة نورد
المثال التالي: إذا حصلنا مثلاً على القيم التالية لتركيز سكر الدم
معبَّراً عنه بالـ مغ/100 مل: 88 89 89 90 91 92 93، فإن القيمة المتوسطة تظهرها
العلاقة المبينة أدناه:
وأما القيمة
الناصفة (التي تقع في منتصف السلسلة) فهي 90؛ وأما القيمة السائدة (التي يتكرر
ظهورها أكثر) فهي 89.
هذا وبالإضافة إلى القيـمة المتوسـطة فإن
|
 |
هناك مَعْلماً آخر
يميِّز منحنى توزع التواتر، ألا وهو الانحراف المعياريّStandard deviation، الذي هو عبارة عن القيمة الممثَّلة بجزء من النتائج يقع على محور
السينات بين النقطة التي تقع مباشرة تحت ذروة المنحنى، أي الممثِّلة للقيمـة
المتوسـطة، والنقطة التي تقع مباشـرة تحت نقطـة انعطـافPoint of Inflection المنحنى التي يتحول عندها تقعُّر المنحنى إلى تحدُّب أو تحدُّبه
إلى تقعُّر، أي النقطة التي يكون مماس المنحنى عندها متقاطعاً مع المنحنى (انظر
الشكل 2 السابق). ويُرمَز للانحراف المعياريّ بالحرف s أو الحرفين SD، وأحياناً بالحرف الإغريقي σ (سيغما).
الانحراف المعياريّS هو معيار لتبعثر Dispersion القيم المَقيسة حول القيمة المتوسطة ()، ويُحسَب رياضياً بتعيين القيمة المتوسطة وحساب الفرق بين كل
نتيجـة والقيمـة المتوسـطة ( )، ثم تربيع هذا الفرق ، وحساب مجموع مربعات الفروق
كلها 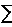، وبعدها تقسيم هذا المجموع على ما يسمى درجة
الحرية (Degree of freedom)،
التي تمثِّل عدد القياسات ( n ) مطروحاً منه العدد 1، أي تمثل ( n – 1)، وأخيراً حساب الجذر التربيعي لحاصل القسمة. وهكذا فإن الانحراف
المعياريّ يعطى بالعلاقة:
 
وباعتبار أن القيمة المتوسطة تعطى
بالعلاقة:
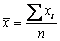
فإن علاقة الانحراف المعياري يمكن أن
تؤول إلى الشكل التالي المفضَّل للحساب بالآلة الحاسبة:
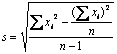
حيث أن: = مجموع مربعات النتائج،  = مربع مجموع النتائج.
هذا وإن مربع الانحراف
المعياري، الذي يساوي حاصل القسمة الموجود تحت الجذر التربيعي في العلاقة السابقة،
يدعى التفاوت Variance، ويشار إليه بالرمز s2 أو σ2. وهكذا فإن الانحراف المعياري يمثِّل الجذر التربيعي للتفاوت.
وبالإضافة
إلى القيمة المتوسطة والانحراف المعياري، فإن هناك مَعْلماً إحصائياً هاماً آخر هو
مُعامِل الاختلاف (معامل التباين) أو الانحراف النسبي المئويCoefficient of variation or
relative standard deviation، وهو عبارة عن الانحراف المعياري محسوباً كنسبة مئوية من القيمة
المتوسطة، ويشار إليه بالرمز CV أو RSD.
وهكذا فإن معامل الاختلاف يعطى بالعلاقة:
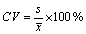
وكمثال على طريقة حساب الانحراف المعياري ومعامل
الاختلاف نستخدم سلسلة النتائج، التي تم على أساسها إعداد منسَّج توزُّع التواتر
الوارد آنفاً. ولتسهيل الحساب نُعِدّ أربعة أعمدة يتضمن أولها من اليسار أرقام
النتائج المتسلسلة، ويشمل العمود الثاني النتائج 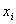 ، وأما العمود الثالث فيتضمن ()، وأما العمود الرابع فيحتوي على: |
| No. () |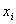
1 47 -3 9
2 48 -2 4
3 48 -2 4
4 49 -1 1
5 49 -1 1
6 49 -1 1
7 49 -1 1
8 50 0 0
9 50 0 0
10 50 0 0
11 50 0 0
12 50 0 0
13 50 0 0
14 51 +1 1
15 51 +1 1
16 51 +1 1
17 51 +1 1
18 52 +2 4
19 52 +2 4
20 53 +3 9 |
 =
|
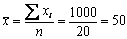
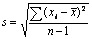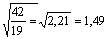
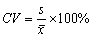
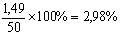
فكيف يميِّز
الانحرافُ المعياري منحنى توزُّع التواتر السويّ (منحنى غاوس). إن المساحة التي
توجد تحت المنحنى بين الانحراف المعياري ((–s، الأقل من القيمة المتوسطة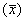 ، والانحراف المعياري (+s)، الأكبر من هذه القيمة، أي المساحة التي تقع ضمن المجال  ، تتضمن حوالي 68% من النتائج، وبالضبط 68.26% (الشكل 2). ومن جهة أخرى فإن المساحة
الأكبر، التي تقع ضمن المجال 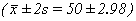 ، والتي تؤلِّف المساحة السابقة جزءاً هاماً منها، تشمل نحو 95% من النتائج، وبالضبـط 95.46%. ومن ناحية ثالثة فإن المساحة الأكبر،
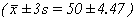التي تشغل المجال  ، والتي تؤلف المساحتان السابقتان الجزء الأعظم منها، تتضمن حوالي
99.7% من النتائج، وبالضبط
99.74%.
هذا وإن العلاقة
المذكورة بين الانحراف المعياري ومنحنى توزُّع التواتر يسري مفعولها فقط في حال التوزُّع
السويّ (توزُّع غاوس) الذي يتسم بالتناظر حول القيمة المتوسطة، وكذلك بوجود ذروة
واحدة فقط، والذي يُعَدّ التوزُّع الغالب، ولكنه ليس الوحيد؛ إذ أن هناك توزعات
شاذة ناجمة على الأغلب عن وجود عيوب في الطريقة المستخدمة أو في تطبيقها.
ومن العيوب التي تُلاحَظ
خلال تطبيق الطرق عيب نفسي يتمثل في مَيل القائم بالتحليل إلى تكرار قيم تم الحصول
عليها مسبقاً، وذلك بسبب تأثره بتلك القيم عن وعي أو دون وعي.
ومن تلك العيوب أيضاً
إجراء الاختبارات في درجتَي حرارة مختلفتين، الأمر الذي من شأنه أن يؤدي إلى تركز
النتائج حول قيمتين مختلفتين، وبالتالي الحصول على توزع ذي ذروتين.
إن الانحراف المعياري (s) ومعامل الاختلاف (CV) هما معياران لدِقَّة النتائجPrecision of results، فكلما كانت قيمتاهما أصغر كانت
الدقة أفضل.
ويدل
الانحراف المعياري ذو القيمة الأخفض على تبعثر أصغر للنتائج حول القيمة المتوسطة،
أي على توزع جيد (سويّ) للنتائج حول هذه القيمة.
وخلافاً للانحراف
المعياري فإن لمعامل الاختلاف مَزِيّة إضافية تتمثل في أنه يمكِّن من المقارنة بين
الطرق التي تم بوساطتها الحصول على النتائج المعنية. ولإيضاح ذلك نفترض أنه لدى
تعيين الصوديوم والبوتاسيوم في مصل الدم بالقياس الضوئي اللهبي تم الحصول على
القيمتين المتوسطتين 140 ممول/ل و 5 ممول/ل على التوالي مع الانحرافين المعياريين
2 ممول/ل و 0.1 ممول/ل على التوالي أيضاً؛ فبناءً على هذه المعطيات نلاحظ أن:
معامل الاختلاف
للصوديوم هو:
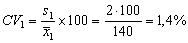
معامل الاختلاف للبوتاسيوم هو:
وهكذا
نرى أن تعيين الصوديوم هنا ذو كفاءة أفضل بسبب أنه ذو معامل اختلاف أصغر على الرغم
من أنه ذو انحراف معياري أكبر.
وهناك
قيم محددة لمعامل الاختلاف لكل مَعلَم من المَعالِم المخبرية، تعتمدها برامج ضبط
الجَوْدة في العمل المخبري، ويجب عدم تجاوزها، وإلا كانت النتائج غير مقبولة
سريرياً.
|
| المراجع References |
1-Bauer J.D.
Clinical Laboratory Methods. Ninth Edition. The C.V. Mosby Company, St. Louis, Toronto, London, 4-12, 1982.
2-Burtis C.A. and Ashwood Tietz E.R.
Textbook of Clinical Chemistry. Second Edition. W.B. Saunders Company, 1994.
3-Campbell J.M. and Campbell. J.P.
Laboratory Mathematics, Medical and Biological Application. 103-177.
4-Department of Clinical Laboratory, Medical academy, Sofia. Instructions for Quality Control, Bulgarian, 1977.
5-Dochev D.
Clinical Laboratory. Medicina i fizkultura, Sofia, 10, 16-18, 21-22, 26 (Bulgarian). 1983.
6-Dochev D; Shipkov T. et al.
Laboratory Diagnostics, Hematological Investigations. Medicina i fizkultura, Sofia, 224-251 (Bulgarian), 1988.
7-Filipovich I. and Sabioncello P.
Laboratory Testbook, part 1, book 3. Tehnichka kniga, Zagreb, 430-458 (Serbocroatian). 1965.
8-Geigy J.R.
Scientific Tables.
Sixth Edition. Edited by Konrad Diem, 32-53, 145-195 (Statistical Methods), 1962.
9-Henry J.B.
Clinical Diagnosis and Management by Laboratory Methods. Twentieth Edition. W. B. Saunders Company. A Harcourt Health Sciences
Company, 138-156, 2001.
10-Henry R.J; Cannon D.C. and Winkelman J.W.
Clinical Chemistry, Principles and Technics. Second Edition. Harper and Row, Publishers, Inc., 289-339, 1974.
11-Kaplan L.A; Pesce A.J. and Kazmierczak S.C.
Clinical Chemistry, Theory, Analysis and Correlation.
Third Edition. Mosby, USA, 342-423, 1996.
12-Karakashov A. and Pandov H.
Clinical Laboratory. Medicina i fizkultura, Sofia, 92-126 (Bulgarian), 1970.
13-Mukherjee K.L.
Medical Laboratory Technology. Vol. I. Tenth Reprint. Tata McGraw-Hill Publishing Company, New Delhi, 199-211, 1995.
14-Randox Laboratories LTD. Randox International Quality Assessment Scheme, Action Guidance Notes.
15-Stam D.
Guidelines for a Basic Program for Internal Quality Control of Quantitative Analyses in Clinical Chemistry. World Health
Organization, LAB/81. 3.
16-Tietz N.W.
Textbook of Clinical Chemistry. W.B. Saunders Company, Philadelphia, 287-355, 424-456, 1986.
17-Varley H. et al.
Practical Clinical Biochemistry. Volume 1. Fifth Edition. William Heinemann Medical Books LTD, London, 338-342.
18-Whitehead T. P.
Principles of Quality Control. World Health Organization, LAB/76. 1.
|
| |
| المجلد 4 , العدد 4 , ذو الحجة 1427 - كانون الثاني (يناير) 2007 |
|
|
|
